2015年05月26日 00:00
ふと思いついたので書いてみた。
呼び出すと、Wレジスタの値を浮動小数点数として見た量だけウェイトを掛ける。
具体的には、指数部3bit、仮数部5bitで、
1.仮数×2^(指数+4)
または指数部が0の時
0.仮数×2^(1+4)
で表される値×80。
最小が1の時の80、最大が255の時の322560…かと思いきやちょうど上手く0の時に327680になっている。
グラフにするとこうだ。
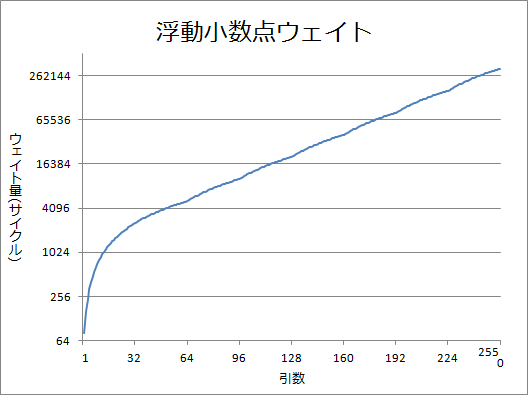
さて、ふと思いついて面白そうだったので書いてみたのだが、使い道が思いつかない。
思いついたきっかけは液晶モジュールの初期化時に27μsと1msと200msのようなウェイト量を要求されたからなのだが、数回使うくらいなら固定値のウェイトルーチンで済むし、10回程度までは単純な2バイトのウェイトルーチンを作った方がよいだろう。
役立てるには数十回のダイナミックレンジの広いウェイトを要求される必要があるが、そのような状況が思いつかない。
まあ書いてて楽しかったので特に問題はない。
何か使い道を思いついた方はご自由に使ってください。
呼び出すと、Wレジスタの値を浮動小数点数として見た量だけウェイトを掛ける。
具体的には、指数部3bit、仮数部5bitで、
1.仮数×2^(指数+4)
または指数部が0の時
0.仮数×2^(1+4)
で表される値×80。
最小が1の時の80、最大が255の時の322560…かと思いきやちょうど上手く0の時に327680になっている。
グラフにするとこうだ。

さて、ふと思いついて面白そうだったので書いてみたのだが、使い道が思いつかない。
思いついたきっかけは液晶モジュールの初期化時に27μsと1msと200msのようなウェイト量を要求されたからなのだが、数回使うくらいなら固定値のウェイトルーチンで済むし、10回程度までは単純な2バイトのウェイトルーチンを作った方がよいだろう。
役立てるには数十回のダイナミックレンジの広いウェイトを要求される必要があるが、そのような状況が思いつかない。
まあ書いてて楽しかったので特に問題はない。
何か使い道を思いついた方はご自由に使ってください。
fwait:
;使用レジスタ:
;cnth, cntl, exp
;cnthは事前にゼロクリアのこと。
;浮動小数点数を分解して適切な場所に置いたりケチ表現解除
movwf cntl
andlw 0xE0
movwf exp
btfss STATUS,Z
bsf cnth,1
btfss cnth,1
bsf exp,5
btfsc cntl,4
bsf cnth,0
swapf cntl,F
movlw 0xF0
andwf cntl,F
bcf STATUS,C
;指数部が1xxなら4bit左シフト
btfss exp,7
goto f1x4
swapf cnth,F
swapf cntl,F
movf cntl,W
andlw 0x0F
iorwf cnth,F
movlw 0xF0
andwf cntl,F
f1:
;指数部がx1xなら2bit左シフト
btfss exp,6
goto f2x1
rlf cntl
rlf cnth
rlf cntl
rlf cnth
f2:
;指数部がxx1でなければ1bit右シフト
btfss exp,5
rrf cnth,F
btfss exp,5
rrf cntl,F
;素通りに掛かる時間分の調整
movlw .8 ;40/5
subwf cntl,F
btfsc STATUS,C
incf cnth,F ;繰り下がり処理しつつ+1
b0:
;時間待ち処理本体
;ここにウェイトを入れ、上の調整部分も合わせると、全体のウェイト量を定数倍できる
decf cntl,F
btfsc STATUS,Z
decfsz cnth,F
goto b0
nop ;時間調整
retlw 0
;分岐の時間合わせ
f2x1:
nop
goto f2
f1x4:
goto $+1
goto $+1
goto f1
;使用レジスタ:
;cnth, cntl, exp
;cnthは事前にゼロクリアのこと。
;浮動小数点数を分解して適切な場所に置いたりケチ表現解除
movwf cntl
andlw 0xE0
movwf exp
btfss STATUS,Z
bsf cnth,1
btfss cnth,1
bsf exp,5
btfsc cntl,4
bsf cnth,0
swapf cntl,F
movlw 0xF0
andwf cntl,F
bcf STATUS,C
;指数部が1xxなら4bit左シフト
btfss exp,7
goto f1x4
swapf cnth,F
swapf cntl,F
movf cntl,W
andlw 0x0F
iorwf cnth,F
movlw 0xF0
andwf cntl,F
f1:
;指数部がx1xなら2bit左シフト
btfss exp,6
goto f2x1
rlf cntl
rlf cnth
rlf cntl
rlf cnth
f2:
;指数部がxx1でなければ1bit右シフト
btfss exp,5
rrf cnth,F
btfss exp,5
rrf cntl,F
;素通りに掛かる時間分の調整
movlw .8 ;40/5
subwf cntl,F
btfsc STATUS,C
incf cnth,F ;繰り下がり処理しつつ+1
b0:
;時間待ち処理本体
;ここにウェイトを入れ、上の調整部分も合わせると、全体のウェイト量を定数倍できる
decf cntl,F
btfsc STATUS,Z
decfsz cnth,F
goto b0
nop ;時間調整
retlw 0
;分岐の時間合わせ
f2x1:
nop
goto f2
f1x4:
goto $+1
goto $+1
goto f1
2015年05月06日 23:32
なんとなく欲しくなったので作ってみたらできた気がする。
valh:vallに平方根を求める値を入れる。vallに答えが出る。
このルーチンに入る前にcountはゼロにしておく。
入力は16bitを受け付けてくれるかと思いきや、大きすぎると計算途中でオーバーフローするようである。
15bitなら多分大丈夫。もうちょっと大きくても大丈夫な気がする。0b1011...まで大丈夫な気がしたがそんなことはなかった。
こちらのタイガー計算器での開平計算のアルゴリズムを参考にした。
同じことを2進法で行うのだが、2進法なので引く数を増やしながら順に引いていくところは1回だけで終わりである。
具体的には、
コードに落としこむにあたって、引けた時と引けなかった時の計算に使う値を1つにまとめたのと、キャリーを壊さずに後の方まで使いまわしているのが楽しいところ。
引く数は最後の方は下位bitを切り捨てているので答えが多少ずれるだろうと思っていたのだが、いくつか試したところずれていないような気がする。不思議だ。
(5/7追記: √0が1になった。やっぱりなー。この程度は想定の範囲内。)
sqrt:
movlw 0x60
movwf diff
movlw 0x40
movwf subhnd
bsf count,3
sqrtloop:
movf subhnd,W
subwf valh,W
btfsc STATUS,C
movwf valh
movf diff,W
rlf vall,F
rlf valh,F
rrf diff,F
btfss vall,0
xorwf subhnd,F
btfsc vall,0
addwf subhnd,F
decfsz count,F
goto sqrtloop
19命令、固定124サイクル。movlw 0x60
movwf diff
movlw 0x40
movwf subhnd
bsf count,3
sqrtloop:
movf subhnd,W
subwf valh,W
btfsc STATUS,C
movwf valh
movf diff,W
rlf vall,F
rlf valh,F
rrf diff,F
btfss vall,0
xorwf subhnd,F
btfsc vall,0
addwf subhnd,F
decfsz count,F
goto sqrtloop
valh:vallに平方根を求める値を入れる。vallに答えが出る。
このルーチンに入る前にcountはゼロにしておく。
入力は16bitを受け付けてくれるかと思いきや、大きすぎると計算途中でオーバーフローするようである。
15bitなら多分大丈夫。もうちょっと大きくても大丈夫な気がする。0b1011...まで大丈夫な気がしたがそんなことはなかった。
アルゴリズム
平方根の求め方 - 魔法使いの森こちらのタイガー計算器での開平計算のアルゴリズムを参考にした。
同じことを2進法で行うのだが、2進法なので引く数を増やしながら順に引いていくところは1回だけで終わりである。
具体的には、
・平方根を求める数をAとする
・B=1
{
・Aの2nビット目からBを引き、キャリーを答にシフト (そのまま使えるのでPICのボローは楽である)
・引けたなら、B++; B<<1; B++
・引けなかったなら、B--; B<<1; B++
・A<<2
}繰り返し
なお図形的に考えたものに合わせAとB両方シフトするように書いたが、実際にはAを1bitシフト、Bを右に伸ばしていくようなコードになっている。これはタイガー計算器でもそうである。・B=1
{
・Aの2nビット目からBを引き、キャリーを答にシフト (そのまま使えるのでPICのボローは楽である)
・引けたなら、B++; B<<1; B++
・引けなかったなら、B--; B<<1; B++
・A<<2
}繰り返し
コードに落としこむにあたって、引けた時と引けなかった時の計算に使う値を1つにまとめたのと、キャリーを壊さずに後の方まで使いまわしているのが楽しいところ。
引く数は最後の方は下位bitを切り捨てているので答えが多少ずれるだろうと思っていたのだが、いくつか試したところずれていないような気がする。不思議だ。
(5/7追記: √0が1になった。やっぱりなー。この程度は想定の範囲内。)







